Factorización

Diferencia de cuadrados perfectos: es una expresión que consta de dos términos, los cuales son cuadrados perfectos, es decir tienen raíz cuadrada exacta cada uno, la diferencia de cuadrados perfectos es igual al producto de la suma por la diferencia de sus bases.

Los pasos para desarrollar la diferencia de cuadrados perfectos son :

 1)   Extraer la raíz cuadrada de ambos términos.
 2)   Se multiplica la suma por la diferencia de estas cantidades.

Ejemplos;

1)  9x² - 16y² 
Para ser diferencia de cuadrados debe cumplir que ambos terminos tienen raiz cuadrada exacta y deben estar separados por el signo menos.

√9x² = 3x
√15y² = 4x      Cumple las condiciones, luego 9x² - 16y² es una diferencia de cuadrados

Su factorizacion es:
9x² + 16y³ = (3x +4y)(3x - 4y)

Ver más en Brainly.lat - https://brainly.lat/tarea/1078434#readmore

2)   x² - 9 = (x + 3)*(x - 3)

3)  x² - y² = (x + y)*(x - y)

4)  x² - 9/25 = (x + 3/5).(x - 3/5)

5) 36x² - a⁶b⁴ = (6x + a³b²).(6x - a³b²)

6) x² - 4/25 = ( x + 2/5)* ( x -2/5)

La diferencia de cuadrados perfectos  es un caso de factorización, el cual se reconoce por la expresión que está formada por la diferencia de dos términos y dichos términos son cuadrados perfectos, es decir poseen raíz cuadrado exacta.

Factorizacion por factor comun

Extraer factor común de una suma (o resta) consiste en escribirla como un producto. Por ejemplo,

Ejemplo 1

En la suma $3\cdot y+3\cdot x$ tenemos el factor común 3. Podemos extraerlo: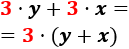

Observad que lo que hacemos es aplicar la propiedad distributiva del producto sobre la suma.
No olvidéis nunca los paréntesis porque el factor común debe multiplicar a todos los sumandos.

Extraer factor común nos permite simplificar las expresiones aritméticas, por lo que es algo que debemos hacer con habilidad.

Actividad; realizar las siguientes operaciones de diferencia de cuadrado en su cuaderno.

a.    16x²  -  9y²  =

b.    144a²  -  100b²  = 

c.    121  -  x⁴  =

d.    225p⁴  -  49a⁴y⁶z⁸  =

e.    100m²  -  81a²b⁴  =

Extraer el factor común  de las siguientes sumas:

1. ab8 – 7a³b² – ab6 + a²b5.
2. 5ab + 7a
3. 5x² + 3xy – 4x
4. x² + 3x³y + 4x 
5. 8+2x2+12x