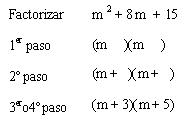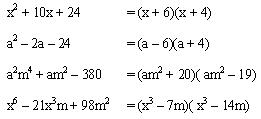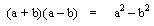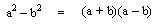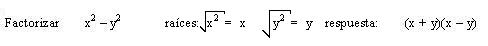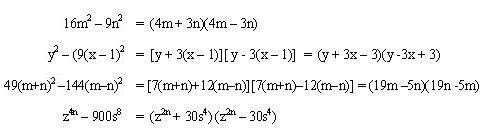Matemática Diversificado
lunes, 8 de junio de 2020
martes, 12 de mayo de 2020
Trinomio de la forma x²+bx+c
- Posee un termino que tiene la misma letra que el termino anterior pero elevada a 1 (bx) (puede ser negativo o positivo).
- Tienen un termino independiente de la letra que aparece en los otros dos (+ o -).
- El trinomio debe estar organizado en forma descendente.
- El coeficiente del primer término debe ser uno (1).
- El grado (exponente) del primer término debe ser el doble del grado (exponente) del segundo término.
Cómo realizar la factorización
- Se abren dos grupos de paréntesis.
- Se le extrae la raíz cuadrada al primer término y se anota al comienzo de cada paréntesis.
- Se definen los signos: el signo del primer paréntesis se obtiene al multiplicar los signos del primer y segundo término; el signo del segundo paréntesis se obtiene al multiplicar los signos del segundo y tercer término.
- Buscamos dos cantidades que multiplicadas den como resultado el término independiente (es decir c), y que sumadas den como resultado el coeficiente del segundo término (es decir b).
- Se anotan las cantidades que satisfacen las condiciones anteriores en los espacios en blanco de cada paréntesis, en sus lugares respectivos.
Ejemplos
ACTIVIDAD: escribir un breve concepto en su cuaderno sobre el tema y realizar 4 ejercicios de los siguientes.
| 01) | x2 + 8x + 15 | |
| 02) | n2 + n - 20 | |
| 03) | m2 - 12m + 27 | |
| 04) | x2 - 2x - 24 | |
| 05) | x2 + 20x + 75 | |
| 06) | y2 + 16y - 80 | |
| 07) | x2 - 25x + 100 |
martes, 28 de abril de 2020
Factorización de un Trinomio Cuadrado Perfecto
Características y cuándo aplicarlo
- El trinomio debe estar organizado en forma ascendente o descendente (cualquiera de las dos).
- Tanto el primero como el tercer término deben ser positivos. Asimismo, esos dos términos deben ser cuadrados perfectos (es decir, deben tener raíz cuadrada exacta). En otras palabras, el primero y el tercer término deben reunir las características de los términos que conforman una Diferencia de Cuadrados Perfectos.
Cómo realizar la factorización
- Primero debemos verificar que se trata de un Trinomio Cuadrado Perfecto (TCP). Para ello extraemos la raíz cuadrada tanto del primer como del tercer término.
- Realizamos el doble producto de las raíces obtenidas y comparamos con el segundo término (sin fijarnos en el signo de éste). Si efectivamente nos da, entonces tenemos un TCP.
- La factorización de un TCP es un binomio al cuadrado, que se construye anotando las raíces cuadradas del primer y tercer término, y entre ellas el signo del segundo término.
Ejemplos
- El trinomio debe estar organizado en forma ascendente o descendente (cualquiera de las dos).
- Tanto el primero como el tercer término deben ser positivos. Asimismo, esos dos términos deben ser cuadrados perfectos (es decir, deben tener raíz cuadrada exacta). En otras palabras, el primero y el tercer término deben reunir las características de los términos que conforman una Diferencia de Cuadrados Perfectos.
Cómo realizar la factorización
- Primero debemos verificar que se trata de un Trinomio Cuadrado Perfecto (TCP). Para ello extraemos la raíz cuadrada tanto del primer como del tercer término.
- Realizamos el doble producto de las raíces obtenidas y comparamos con el segundo término (sin fijarnos en el signo de éste). Si efectivamente nos da, entonces tenemos un TCP.
- La factorización de un TCP es un binomio al cuadrado, que se construye anotando las raíces cuadradas del primer y tercer término, y entre ellas el signo del segundo término.
Ejemplos
Ejemplo 1: a2 – 2ab + b2
Raíz cuadrada de a2 = a
Raíz cuadrada de b2 = b
Doble producto sus raíces
(2 X a X b) 2ab (cumple)
R: (a – b) 2
Ejemplo 2: 49m 6– 70 am3n2 + 25 a2n4
Raíz cuadrada de 49m6 = 7m3
Raíz cuadrada de 25a2n4 = 5an2
Doble producto sus raíces
(2 X 7m3 X 5a2n2) = 70am3 n2 (cumple)
R: (7m – 5an2)
Ejemplo 3: 9b2 – 30 ab + 25a2
Raíz cuadrada de 9b2 = 3b
Raíz cuadrada de 25 a2= 5a
Doble producto sus raíces
(2 X 3b X 5a) = 30ab (cumple)
R: (3b - 5a) 2
ACTIVIDAD: Realizar en el cuaderno los siguientes ejercicios de trinomios de cuadrado perfecto escoger 5 de los 10 ejercicios que se le presentan.
Ejercicios de practica
- 4 – 4x + x2
- 4x2 + 12x + 9
- x2y2 + 8xy +16
- 25m2 – 10mn + n2
- m2n2 + 10mn + 25
- 36x2 – 108x + 81
- 9m2 + 12mn + 4m2
- m2 + 4mn + 4n2
- 9x4 – 30x3y + 25xy
- 16m8 – 64m5n – 64m2n2
martes, 21 de abril de 2020
Factorización
Diferencia de cuadrados perfectos: es una expresión que consta de dos términos, los cuales son cuadrados perfectos, es decir tienen raíz cuadrada exacta cada uno, la diferencia de cuadrados perfectos es igual al producto de la suma por la diferencia de sus bases.
Los pasos para desarrollar la diferencia de cuadrados perfectos son :
1) Extraer la raíz cuadrada de ambos términos.
2) Se multiplica la suma por la diferencia de estas cantidades.
Ejemplos;
1) 9x² - 16y²
Para ser diferencia de cuadrados debe cumplir que ambos terminos tienen raiz cuadrada exacta y deben estar separados por el signo menos.
√9x² = 3x
√15y² = 4x Cumple las condiciones, luego 9x² - 16y² es una diferencia de cuadrados
Su factorizacion es:
9x² + 16y³ = (3x +4y)(3x - 4y)
Ver más en Brainly.lat - https://brainly.lat/tarea/1078434#readmore
3) x² - y² = (x + y)*(x - y)
4) x² - 9/25 = (x + 3/5).(x - 3/5)
5) 36x² - a⁶b⁴ = (6x + a³b²).(6x - a³b²)
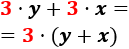
Actividad; realizar las siguientes operaciones de diferencia de cuadrado en su cuaderno.
Los pasos para desarrollar la diferencia de cuadrados perfectos son :
1) Extraer la raíz cuadrada de ambos términos.
2) Se multiplica la suma por la diferencia de estas cantidades.
Ejemplos;
1) 9x² - 16y²
Para ser diferencia de cuadrados debe cumplir que ambos terminos tienen raiz cuadrada exacta y deben estar separados por el signo menos.
√9x² = 3x
√15y² = 4x Cumple las condiciones, luego 9x² - 16y² es una diferencia de cuadrados
Su factorizacion es:
9x² + 16y³ = (3x +4y)(3x - 4y)
Ver más en Brainly.lat - https://brainly.lat/tarea/1078434#readmore
2) x² - 9 = (x + 3)*(x - 3)
3) x² - y² = (x + y)*(x - y)
4) x² - 9/25 = (x + 3/5).(x - 3/5)
5) 36x² - a⁶b⁴ = (6x + a³b²).(6x - a³b²)
6) x² - 4/25 = ( x + 2/5)* ( x -2/5)
La diferencia de cuadrados perfectos es un caso de factorización, el cual se reconoce por la expresión que está formada por la diferencia de dos términos y dichos términos son cuadrados perfectos, es decir poseen raíz cuadrado exacta.
La diferencia de cuadrados perfectos es un caso de factorización, el cual se reconoce por la expresión que está formada por la diferencia de dos términos y dichos términos son cuadrados perfectos, es decir poseen raíz cuadrado exacta.
Factorizacion por factor comun
Extraer factor común de una suma (o resta) consiste en escribirla como un producto. Por ejemplo,
Ejemplo 1
En la suma 3⋅y+3⋅x tenemos el factor común 3. Podemos extraerlo: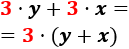
Observad que lo que hacemos es aplicar la propiedad distributiva del producto sobre la suma.
No olvidéis nunca los paréntesis porque el factor común debe multiplicar a todos los sumandos.
No olvidéis nunca los paréntesis porque el factor común debe multiplicar a todos los sumandos.
Extraer factor común nos permite simplificar las expresiones aritméticas, por lo que es algo que debemos hacer con habilidad.
Actividad; realizar las siguientes operaciones de diferencia de cuadrado en su cuaderno.
a. 16x² - 9y² =
b. 144a² - 100b²
=
c. 121 - x⁴ =
d. 225p⁴
- 49a⁴y⁶z⁸ =
e. 100m² - 81a²b⁴ =
Extraer el factor común de las siguientes sumas:
- ab8 – 7a³b² – ab6 + a²b5.
- 5ab + 7a
- 5x² + 3xy – 4x
- x² + 3x³y + 4x
- 8+2x2+12x
jueves, 16 de abril de 2020
..Factorización de una diferencia de cuadrados..
..
Tarea: copiar el concepto base en su cuaderno y como
minimo copiar 4 ejemplos del tema (Videos y concepto escrito),
resolver los siguientes problemas de factorización.
Diferencia de cuadrados
Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.
Al estudiar los Producto Notable teníamos que:
En donde el resultado es una diferencia de cuadrados, para este capítulo es el caso contrario:
Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases.
Pasos a seguir para calcula la diferencia de cuadrados:
- Se extrae la raíz cuadrada de ambos términos.
- Se multiplica la suma por la diferencia de estas cantidades (el segundo termino del binomio negativo es la raíz del termino del binomio que es negativo).
Factorización de una diferencia de cuadrados
La factorización de una diferencia de cuadrados está formada por una ecuación con dos términos: uno positivo y el otro, negativo. Ambos deben de ser raíces cuadradas exactas. Y lo que se hace es realizar una resta entre ellos. De ahí el nombre de factorización por diferencia de cuadrados.
Ejemplos de diferencias de cuadrados
¿Tienes claro ya qué es una diferencia de cuadrados? ¡Te dejamos aquí otros ejemplos para que lo tengas más claro!
Patrón de diferencia de cuadrados
Cada polinomio que sea una diferencia de cuadrados se puede factorizar al aplicar la siguiente fórmula:
a2−b2=(a+b)(a−b)start color #11accd, a, end color #11accd, squared, minus, start color #1fab54, b, end color #1fab54, squared, equals, left parenthesis, start color #11accd, a, end color #11accd, plus, start color #1fab54, b, end color #1fab54, right parenthesis, left parenthesis, start color #11accd, a, end color #11accd, minus, start color #1fab54, b, end color #1fab54, right parenthesis
Observa que, en el patrón, aa y bb pueden ser una expresión algebraica. Por ejemplo, para a=xa, equals, x y b=2b, equals, 2, obtenemos lo siguiente:
x2−22=(x+2)(x−2)
El polinomio x2−4x, squared, minus, 4 ahora se expresa en forma factorizada, (x+2)(x−2)left parenthesis, x, plus, 2, right parenthesis, left parenthesis, x, minus, 2, right parenthesis. Podemos desarrollar el lado derecho de esta ecuación para justificar la factorización:
(x+2)(x−2)=x(x−2)+2(x−2)=x2−2x+2x−4=x2−4
Ahora que entendimos el patrón, usémoslo para factorizar más polinomios.
Ejemplo 1: factorizar x2−16x, squared, minus, 16
Tanto x2x, squared como 1616 son cuadrados perfectos, ya que x2=(x)2x, squared, equals, left parenthesis, start color #11accd, x, end color #11accd, right parenthesis, squared y 16=(4)216, equals, left parenthesis, start color #1fab54, 4, end color #1fab54, right parenthesis, squared. En otras palabras:
x2−16=(x)2−(4)2x, squared, minus, 16, equals, left parenthesis, start color #11accd, x, end color #11accd, right parenthesis, squared, minus, left parenthesis, start color #1fab54, 4, end color #1fab54, right parenthesis, squared
Como los dos cuadrados se están restando, podemos ver que este polinomio representa una diferencia de cuadrados. Podemos usar el patrón de diferencia de cuadrados para factorizar esta expresión:
a2−b2=(a+b)(a−b)start color #11accd, a, end color #11accd, squared, minus, start color #1fab54, b, end color #1fab54, squared, equals, left parenthesis, start color #11accd, a, end color #11accd, plus, start color #1fab54, b, end color #1fab54, right parenthesis, left parenthesis, start color #11accd, a, end color #11accd, minus, start color #1fab54, b, end color #1fab54, right parenthesis
En nuestro caso, a=xstart color #11accd, a, end color #11accd, equals, start color #11accd, x, end color #11accd y b=4start color #1fab54, b, end color #1fab54, equals, start color #1fab54, 4, end color #1fab54. Por lo tanto, nuestro polinomio se factoriza así:
(x)2−(4)2=(x+4)(x−4)
Ejemplo 2: factorizar 4x2−94, x, squared, minus, 9
El coeficiente principal no tiene que ser igual a 11 para usar el patrón de la diferencia de cuadrados. ¡De hecho, el patrón de la diferencia de cuadrados se puede usar en este caso!
La razón es que 4x24, x, squared y 99 son cuadrados perfectos, pues 4x2=(2x)24, x, squared, equals, left parenthesis, start color #11accd, 2, x, end color #11accd, right parenthesis, squared y 9=(3)29, equals, left parenthesis, start color #1fab54, 3, end color #1fab54, right parenthesis, squared. Podemos usar esta información para factorizar el polinomio usando el patrón de la diferencia de cuadrados:
4x2−9=(2x)2−(3)2=(2x+3)(2x−3)
Tarea: copiar el concepto base en su cuaderno y como
minimo copiar 4 ejemplos del tema (Videos y concepto escrito),
resolver los siguientes problemas de factorización.
1)Factoriza x2−25x, squared, minus,problemas de factorización. 25.
2)Factoriza x2−100x, squared, minus, 100.
3)Factoriza 25x2−425, x, squared, minus, 4.
4)Factoriza 64x2−8164, x, squared, minus, 81.
5) Factoriza 36x2−136, x, squared, minus, 1.
6) Factoriza x4−9x, start superscript, 4, end superscript, minus, 9.
7)Factorizar 4x2−49y24, x, squared, minus, 49, y, squared.
Suscribirse a:
Comentarios (Atom)