- Posee un termino que tiene la misma letra que el termino anterior pero elevada a 1 (bx) (puede ser negativo o positivo).
- Tienen un termino independiente de la letra que aparece en los otros dos (+ o -).
- El trinomio debe estar organizado en forma descendente.
- El coeficiente del primer término debe ser uno (1).
- El grado (exponente) del primer término debe ser el doble del grado (exponente) del segundo término.
Cómo realizar la factorización
- Se abren dos grupos de paréntesis.
- Se le extrae la raíz cuadrada al primer término y se anota al comienzo de cada paréntesis.
- Se definen los signos: el signo del primer paréntesis se obtiene al multiplicar los signos del primer y segundo término; el signo del segundo paréntesis se obtiene al multiplicar los signos del segundo y tercer término.
- Buscamos dos cantidades que multiplicadas den como resultado el término independiente (es decir c), y que sumadas den como resultado el coeficiente del segundo término (es decir b).
- Se anotan las cantidades que satisfacen las condiciones anteriores en los espacios en blanco de cada paréntesis, en sus lugares respectivos.
Ejemplos
ACTIVIDAD: escribir un breve concepto en su cuaderno sobre el tema y realizar 4 ejercicios de los siguientes.
| 01) | x2 + 8x + 15 | |
| 02) | n2 + n - 20 | |
| 03) | m2 - 12m + 27 | |
| 04) | x2 - 2x - 24 | |
| 05) | x2 + 20x + 75 | |
| 06) | y2 + 16y - 80 | |
| 07) | x2 - 25x + 100 |

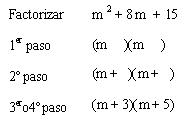
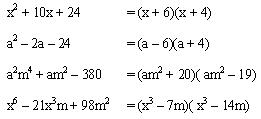
No hay comentarios.:
Publicar un comentario